Разностные уравнения
Многие физические системы моделируются дифферинци-альными уравнениями, например :
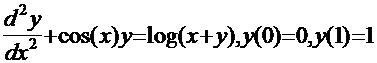
![]()
![]()
![]()
![]()
![]()
![]()
![]() которые не могут быть решены аналитически. Приближение этих уравнений конечными разностями основано на дискредитации интервала [0,1] как показано на рис.1 и замене производной.
которые не могут быть решены аналитически. Приближение этих уравнений конечными разностями основано на дискредитации интервала [0,1] как показано на рис.1 и замене производной.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
простой разностью, например :
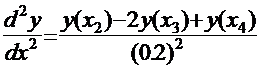
где, 0,2=1/5=X4-X3.
Тогда аппроксимирующее разностное уравнение имеет вид:
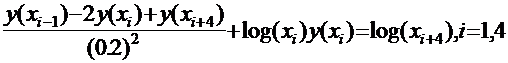
В каждой точке дискретизации справедливо одно такое уравнение, которое приводит к линейной системе для приближенных значений решения дифференциального уравнения.
Уравнения такого вида можно решить с помощью разложения в ряд Тейлора. В нашем случае уравнения решенные разложением в ряд Тейлора имеют вид;
![]()
Найти
y’(0); y’’(0)=1; y’’’(0)=1; ![]()
обозначим у’(0) как С.
Решение:
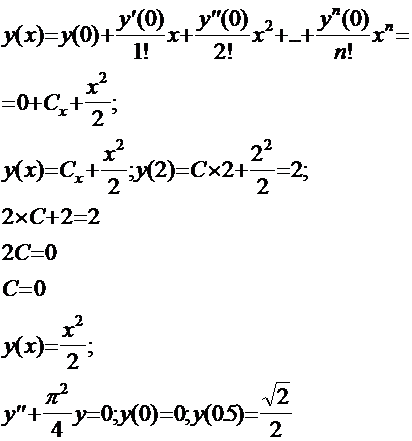
Решение:
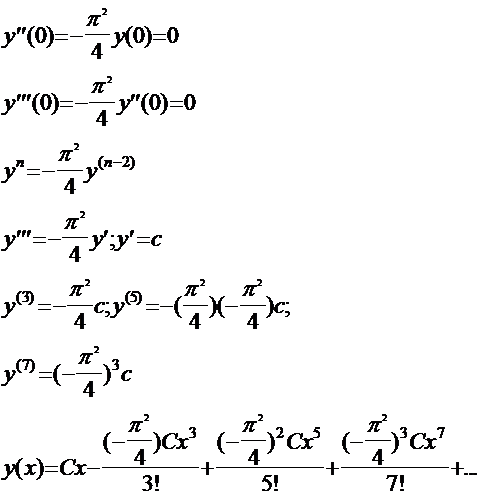
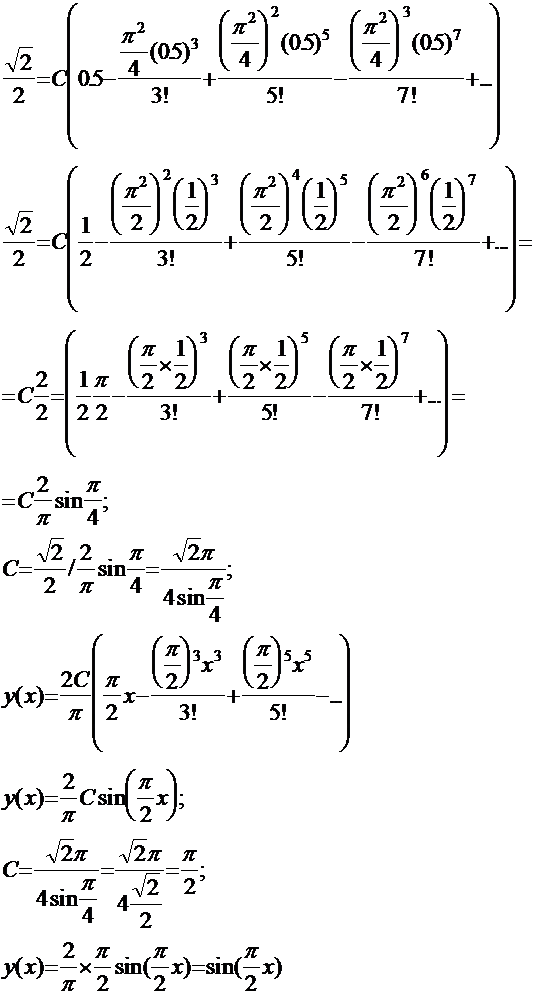
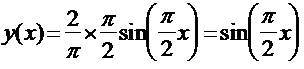
Система конечно-разностных уравнений
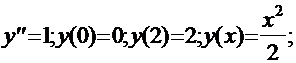
интервал [0,2] разделим на 10 точек
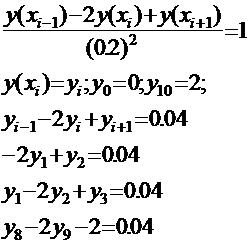
-2 1 0 0 0 0 0 0 0 0 ![]() 0.04
0.04
1 -2 1 0 0 0 0 0 0 0 ![]() 0.04
0.04
0 1 -2 1 0 0 0 0 0 0 ![]() 0.04
0.04
0 0 1 -2 1 0 0 0 0 0 ![]() 0.04
0.04
0 0 0 1 -2 1 0 0 0 0 ![]() 0.04
0.04
0 0 0 0 1 -2 1 0 0 0 ![]() 0.04
0.04
0 0 0 0 0 1 -2 1 0 0 ![]() 0.04
0.04
0 0 0 0 0 0 1 -2 1 0 ![]() 0.04
0.04
0 0 0 0 0 0 0 1 -2 1 ![]() 0.04
0.04
0 0 0 0 0 0 0 0 1 -2 ![]() -2+0.04
-2+0.04
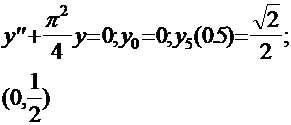
5 точек.
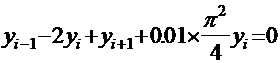
|
|
1 |
0 |
0 |
0 |
|
0 |
|
1 |
|
1 |
0 |
0 |
|
0 |
|
0 |
1 |
|
1 |
0 |
|
0 |
|
0 |
0 |
1 |
|
1 |
|
0 |
|
0 |
0 |
0 |
1 |
|
|
0 |




