На железнодорожном транспорте, в автомобильной промышленности и в других отраслях народного хозяйства нашли широкое применение резинотехнические или пласт­массовые изделия, имеющие, как правило, сложную геометрическую форму. Эти изделия изготавливаются в закрытых тепловых камерах, в которых под высоким давлением и при заданном температурном режиме заготовки изделий выдерживаются строго определённое время. Материал заготовки хоть и обладает конечными упругими характеристиками, но на­ходится в состоянии близкому к пластическому. В течении времени нахождения в тепло­вой камере в результате химических реакций материал приобретает такие упругие свойства, которые делают его работоспособным. Этот процесс перехода пластических свойств в упругие называют вулканизацией. Производство изделий требует точного знания времени пребывания заготовки изделия в тепловой камере, в течении которого изделие прогревается до той температуры, при которой произойдёт вулканизация. Так как материал изделий имеет низкую теплопроводность, время вулканизации в зависимости от толщины изделия может изменятся от нескольких минут до нескольких часов. На рис.1 представлены некоторые геометрические формы изделий, применяющихся в народном хозяйстве.

Для определения времени вулканизации необходимо определить температурное поле изделий при заданных граничных условиях на внутренней и наружной поверхностях изделия (рис.2).

Таким образом задача сводится к решению уравнения теплопроводности при граничных условиях 1-го рода. 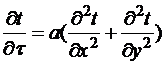(1)

где t – температура в точке с координатами x и у в момент времени t;

а – температуропроводность

Экзотермический эффект вулканизации в данном случае не учитывается, поскольку повышение при этом интенсивности нагрева компенсируется понижением коэффициента теплопроводности, а соответственно и температуропроводности, при повышении температуры нагрева изделия от начальной до температуры вулканизации.

Обычно такие задачи решаются численными методами. Сложность решения задачи заключается в описании геометрической поверхности. В принятой практике для упрощения описания сложной геометрической поверхности изделия используется метод приведенной пластины, который позволяет свести задачу к расчёту температурного поля пластины эквивалентной толщины.

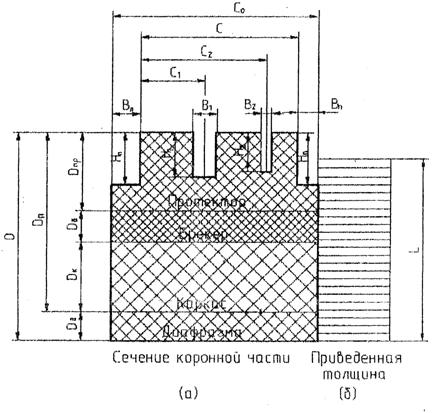
Рис.3 – Приведение к эквивалентной пластине

Приведение осуществляется по зависимости:

L=D-H exp[-092(C/D)1,85] (2)

Где D –толщина коронной части покрышки вместе с диафрагмой;

H – высота шашки по центру покрышки;

L – приведенная толщина;

C –наибольшая ширина шашки в её средней части

Время нагрева изделия длится до того момента, при котором самая минимальная температура по толщине пластины достигнет определённого значения (температуры вулканизации = 140 С).