Рис. 9. Тепловой поток и коэффициент теплоотдачи для двухслойной пластины точки 2.

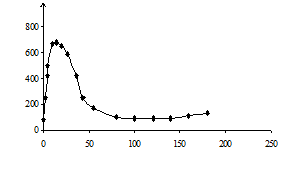
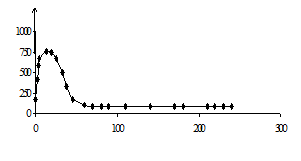
В реальных условиях измеряемые температуры (то есть исходные данные для обратной тепловой задачи) являются случайными величинами из-за дефектов производства, технологии изготовления, загрязнения поверхности, погрешности измерения и обработки экспериментальной информации. Влияние погрешностей исходной информации на решение обратной задачи теплопроводности оценивалось с помощью метода статистических испытаний Монте – Карло / 5-8 /. Анализ результата статистического моделирования решения обратной задачи позволяет установить коридор ошибок искомых граничных условий.

Одним из методов решения ОЗТ является метод статистических испытаний Монте –Карло, который заключается в статистическом моде­лировании аналитических решений ОЗТ с учетом случайного характе­ра исходных данных /121/.

В методе Монте-Карло основным является случайная выборка исходных данных /24/. В данной работе для этого необходим источ­ник случайных чисел.

Введем для исходных данных обозначение

(24)

где - математическое ожидание j – го параметра в точках. Ошибку представим в виде